為什麼需要學習線性回歸?
線性回歸可以被用來預測連續數值，例如：房價預測、股票預測等，只要我們想要解決的問題是線性的。
什麼是線性回歸?
線性回歸是利用方程式的最小平方函數對一個或多個自變數和應變數之間關係進行建模的一種回歸分析，這種函數是一個或多個稱為回歸係數的模型參數的線性組合。

◆簡單回歸(只有一個自變數):
y=β₀+β₁X+ϵ
β₀是截距(常數項)。
β₁是斜率(自變量的係數)。
ϵ 是誤差項，表模型未能捕捉到的變量。
◆多元回歸(大於一個自變數):
y=β₀+β₁X₁+β₂X₂+…+βₙXₙ+ϵ

為了導入 Matplotlib 的繪圖模塊，我們要先安裝 Matplotlib，在命令提示字元中輸入:

pip install matplotlib

確認是否有裝好則輸入:

pip show matplotlib

這樣就成功了。

導入需要的庫:

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

隨機生成一些數據來進行運算實作：

np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

用tf.keras定義模型:

model = tf.keras.Sequential([
    tf.keras.layers.Dense(1, input_shape=(1,))
])

選擇損失函數和優化器:

model.compile(optimizer='sgd', loss='mean_squared_error')

使用 fit 方法來訓練模型:

model.fit(X, y, epochs=100)

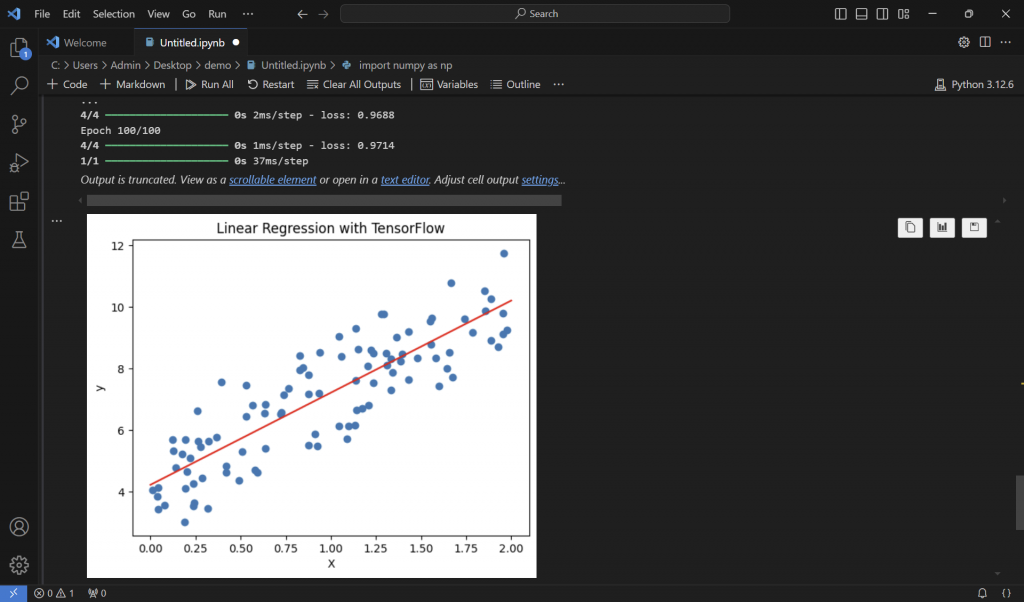
最後用模型進行預測並可視化結果：

X_new = np.array([[0], [2]])
y_predict = model.predict(X_new)
plt.scatter(X, y)
plt.plot(X_new, y_predict, color='red')
plt.xlabel("X")
plt.ylabel("y")
plt.title("Linear Regression with TensorFlow")
plt.show()

最後得到了這張圖: